Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Complement pour l'éléctromagnétique

    Formulaire de report


    Notions générales

    Champ vectoriel

    Vecteurs et pseudo-vecteurs


    Regles sur les vecteurs et pseudo-vecteurs:

    • le sens d'un vecteur polaire (vecteurs) est imposé par définition
    • le sens d'un vecteur axial (pseudo-vecteur) dépend d'une convention

    Règles de symétrie


    Symétrie (nature vectorielle du champ)

    Principe de Currie

    Comportement des vecteurs polaires dans une symétrie par rapport à un plan



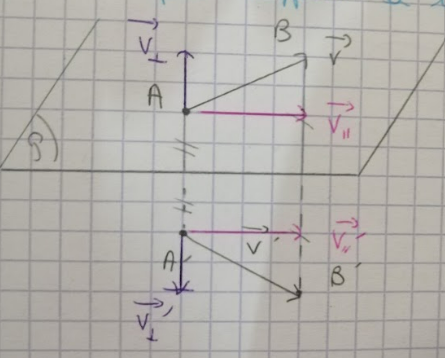
    \(\vec v'=Sym(\vec v)\)
    Un vecteur qui se transforme comme un bipoint est un vrai vecteur (polaire)
    La composante parallèle au plan de symétrie est invariante, alors que la composante perpendiculaire change de signe
    \(\vec v_{\parallel}={{\vec v'_{\parallel} }}\)
    \(\vec v_{\perp}={{-\vec v'_{\perp} }}\)

    Remarque sur les plans

    Un plan contenant toutes les charges est symétrique
    :

    Plans de symétrie:
    • Plan de symétrie du tableau qui contient \(P\), \((\mathcal P_1,P)\) \(\implies\vec E(P)\in \mathcal P1\)
    • Plan de symétrie perpendiculaire au tableau \(\mathcal P_2\) qui contient \(P\) \(\implies \vec E(P)\in \mathcal P_2\).

    Donc: $$\vec E(P)\in \mathcal P_1\cap\mathcal P_2$$
    Etudions le sens:
    Le sens du champ dépend de \(\lambda\), la densité linnéique de charges. (Le champ "fuit les charges positives")
    Si \(\lambda\gt 0\), le champ est perpendiculaire au fil et vers la droite
    Si \(\lambda\lt 0\), le champ est perpendiculaire au fil et vers la gauche.

    Invariances (Les variables du champ)

    Invariances géométrique

    Plan d'antisymétrie

    Plan d'antisymétrie

    Flux et circulation d'un champ vectoriel

    Circulation (vectorielle) Flux (vectoriel)

    Rotationnel, gradient et divergence d'un champ vectoriel

    Rotationnel Opérateur divergence Gradient
    Laplacien

    Localité du gradient sur une surface équipotentielle


    Localité du gradient sur une surface équipotentielle

    D'aprés la relation: \(\vec{grad}f.\vec{dM}=df\)
    Pour une surface ayant le même potentielle en tout point (\(M, M'\)), étudiée localement, on trouve:
    $$\oint \vec{grad}f.\vec{dM}=0$$
    Car, \(f\), le potentielle de (\(\vec{MM'}=\vec {dM}\)), est constante puisque \(df=f(M)-f(M')=0\).
    On déduit alors que \(\vec{dM}\perp\vec{grad}f\)

    Théorèmes

    Théorème de Stokes Théorème d'Ostrogradsky - de la divergence

    Coordonnées

    Coordonnées sphériques

    Bibliographie:

    • Les bases de l'éléctromagnétisme, M.Hulin - J.P. Maury (Dunod)
    • Les ondes éléctromagnétiques, M.Hulin
    • Electromagnétisme: fondements et applications, J.P. Pérez
    • Electrécité et magnétisme, Barkley, A. Collin
    • Les cours de Feynam, éléctromagnétisme